Chapter 7 Total Votes for a Hidden Gem

The following plot shows the distribution of Total Votes for a Hidden Gem.

• Minimum number of votes is 1

• Maximum number of votes is 1246

• Median number of votes is 39

95% Confidence Interval for a Hidden Gem Votes is between 44 and 65

7.1 Box Plot ( without Outliers )

kvcs %>%
  filter(!is.na(TotalVotes)) %>%
  filter( TotalVotes < 400) %>%
      ggplot(aes(x = TotalVotes, fill = fillColor2)) +
      geom_boxplot() + 
      labs(x= ' [Total Votes]',y = ' [Count]', title = paste("Distribution of", ' Total Votes ')) +
      theme_fivethirtyeight() +
  theme(legend.position = "none")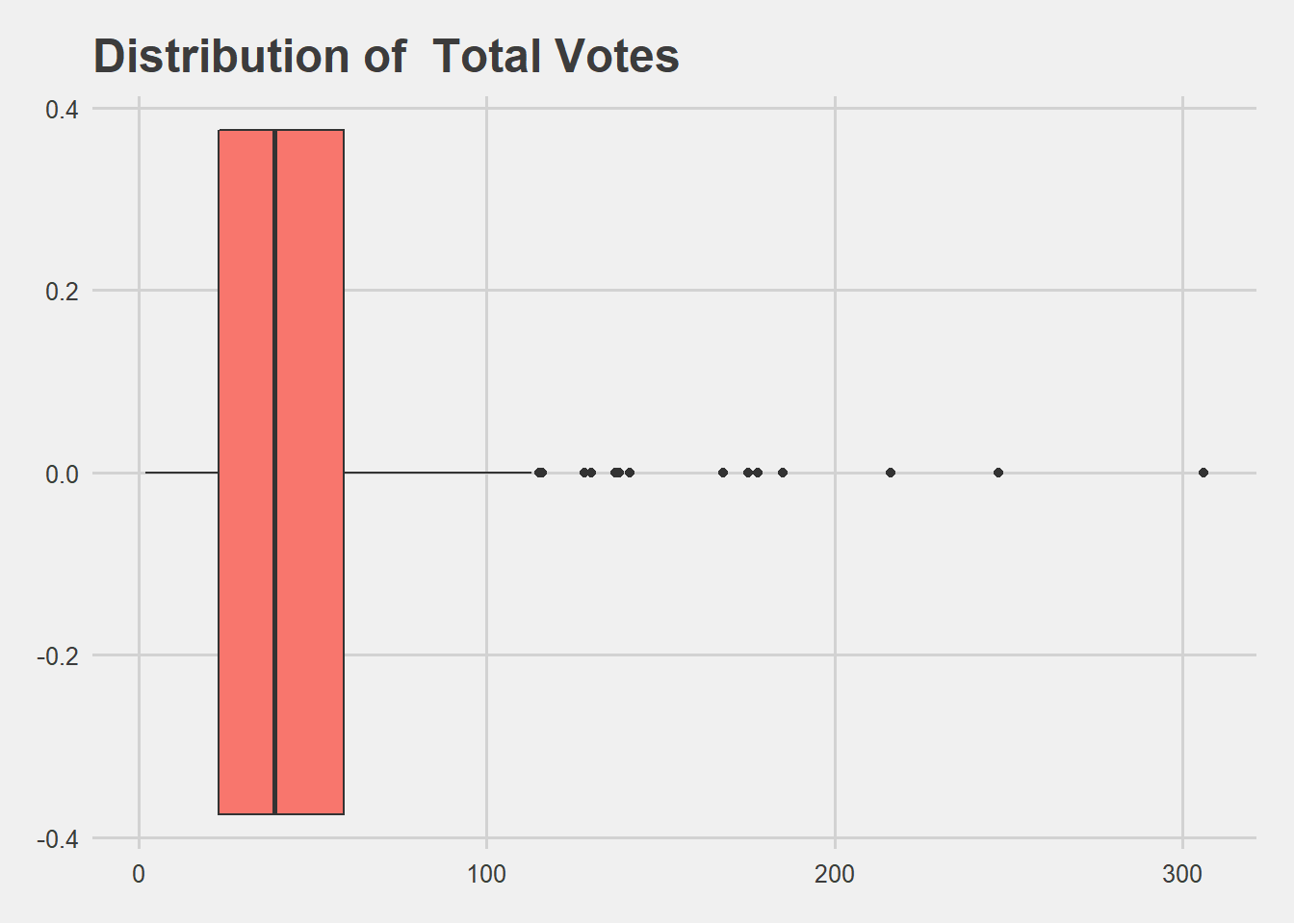 

7.2 Box Plot

kvcs %>%
  filter(!is.na(TotalVotes)) %>%
      ggplot(aes(x = TotalVotes, fill = fillColor2)) +
      geom_boxplot() + 
      labs(x= ' [Total Votes]',y = ' [Count]', title = paste("Distribution of", ' Total Votes ')) +
      theme_fivethirtyeight() +
  theme(legend.position = "none")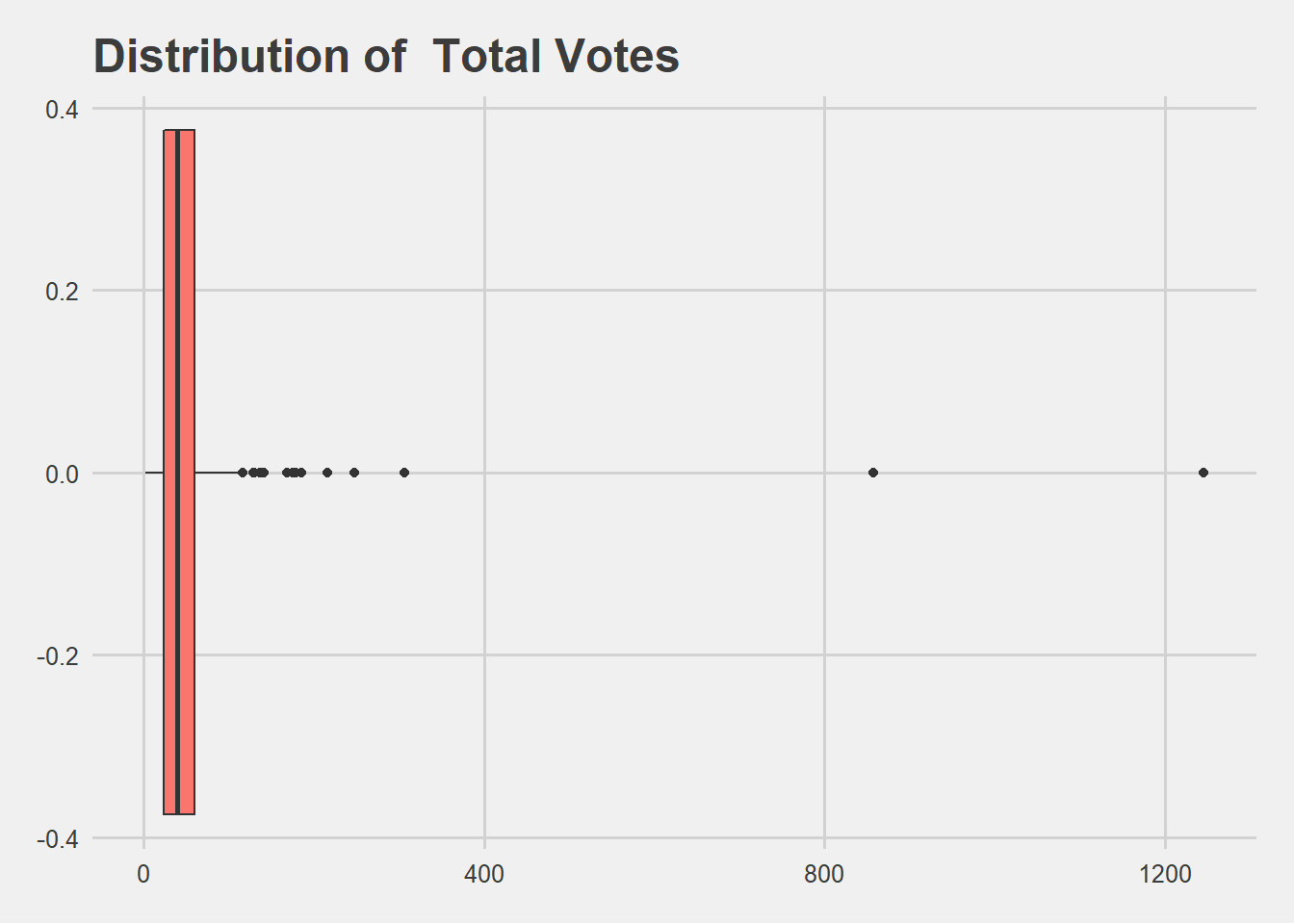 

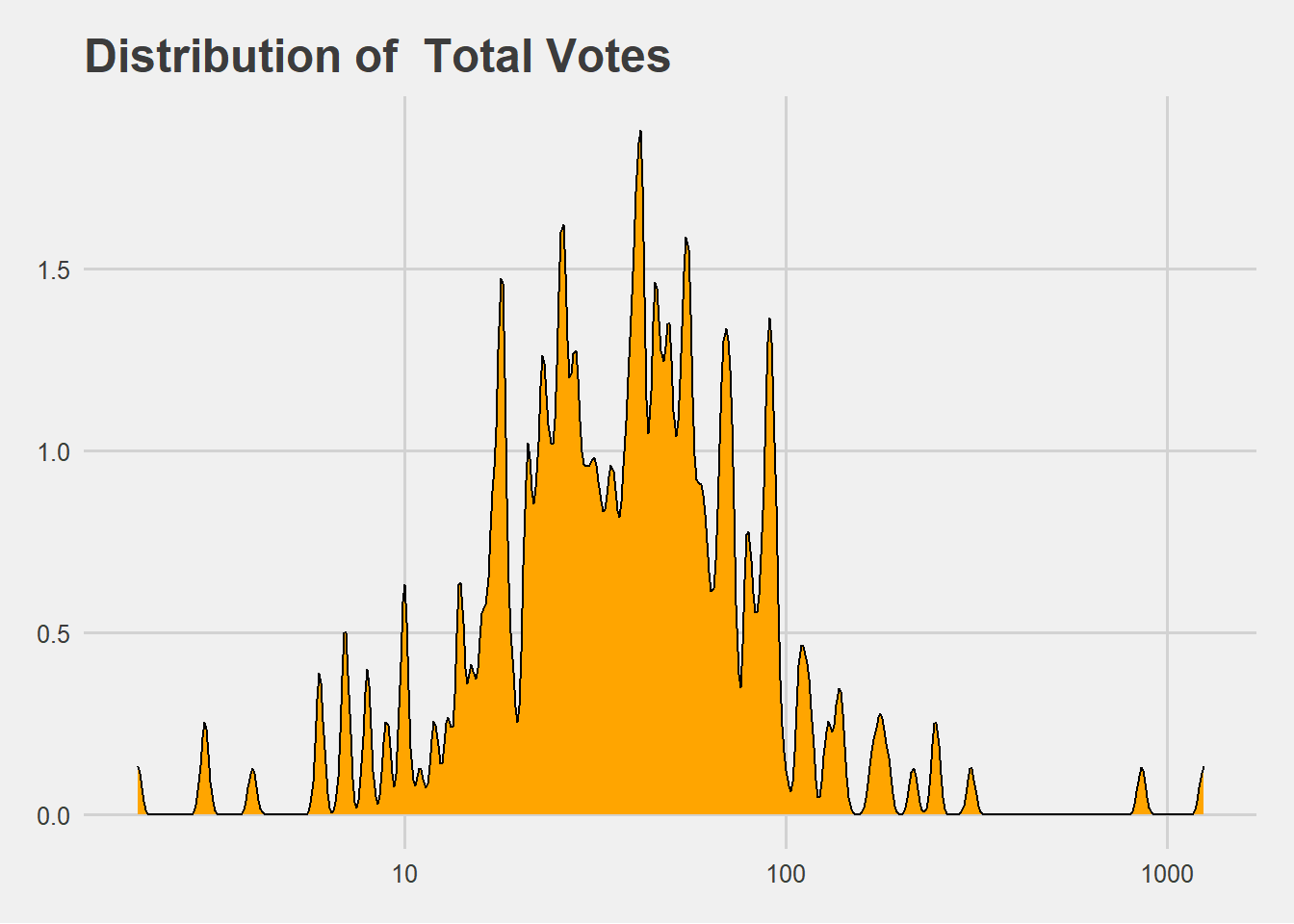
7.3 Density Plot

kvcs %>%
  filter(!is.na(TotalVotes)) %>%
      ggplot(aes(x = TotalVotes, fill = fillColor2)) +
      geom_density(fill = "orange", bw = 0.01) +
      scale_x_log10() +
      labs(x= ' [Log Total Votes]',y = ' [Count]', title = paste("Distribution of", ' Total Votes ')) +
      theme_fivethirtyeight() +
  theme(legend.position = "none") 

7.4 Summary Statistics for Votes

summary(kvcs$TotalVotes)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##    2.00   23.00   39.00   54.64   60.00 1246.00       8

7.5 95% Confidence Interval for Hidden Gems Votes

# Calculate the mean and standard error
l.model <- lm(TotalVotes ~ 1, kvcs)

# Calculate the confidence interval
confint(l.model, level=0.95)

##               2.5 %   97.5 %
## (Intercept) 43.8725 65.40832